– vnútornú ( zákonitosti pohybu strely v hlavni )
– prechodnú ( zákonitosti pohybu strely bezprostredne po opustení ústia hlavne )
– vonkajšiu ( zákonitosti pohybu strely v priestore po opustení hlavne )
– terminálnu ( zákonitosti pohybu strely pri vnikaní do cieľa a prienikom cez cieľ )
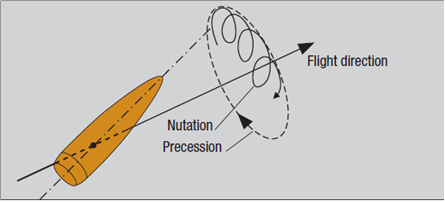Strela pri svojom lete kmitá, pričom jej špička opisuje kružnicu ( nutation ) a pozdĺžna os opisuje okolo dráhy kuželový povrch s vrcholom v ťažisku strely ( precession ). Ďalej je potrebné uviesť najdôležitejšie fyzikálne veličiny. Jednou z nich je prierezová hustota q ( g/mm2 – sectional density ), ktorá je definovaná jako pomer hmotnosti m a prierezovej plochy S strely.
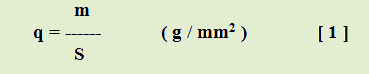
Kinetická energia je jedinou energiou pre deštrukciu cieľa. Na deštrukcii sa nepodieľa celá táto energia, len jej časť – lokálne prenesená energia Eab
Zo vzorca [ 1 ] môžeme odvodiť, že pri pohybe strely a náhlom vzniku uhlu medzi pozdĺžnou osou a smerom jej letu, hodnota q sa znižuje z dôvodu zväčšenia prierezovej plochy strely. Prierezová hustota má tiež velký vplyv na hĺbku prieniku L, pričom hĺbka je priamo závislá na prierezovej hustote a nepriamo prenose energie.
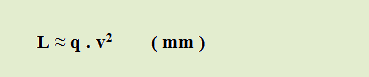
Pozrime sa teraz podrobnejšie na to, čo sa deje zo strelou, v prvom prípade uvažujme s celoplášťovou strelou, v cieli ako je znázornené na ďalšom obrázku ( 2 )
Môžeme tu pozorovať tri oblasti ( 3 ).
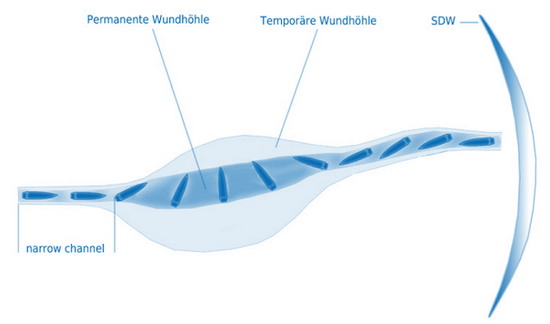
I.oblasť tvorí strelný kanál, ktorý v najužšom mieste dosahuje priemer zodpvedajúci približne 1,5 až 2,5 násobku kalibru strely. Pri vstupe strely do cieľa je na špičke strely vytvorený velký tlak. Viskozita a zotrvačnosť cieľa spôsobí, že iba malá časť povrchu strely zostáva v kontakte s cieľom. Nakoľko je povrch strely v kontakte s cieľom obmezený, sila pôsobí skoro len na špičku strely. Moment preklopenia, ktorý by spôsobil vybočenie strely, závisí hlavne na uhle dopadu. Pri dostatočne stabilnom lete strely je uhol dopadu malý a moment preklopenia je menší ako gyroskopický moment strely. Pri ďalšom pohybe strely sa znižuje jej rychlost, povrchový kontakt s cieľom sa zvyšuje, čo vedie k zvýšeniu sily, následne dochádza k zväčšovaniu uhla nábehu a strela sa prevracia. Dĺžka strelného kanálu závisí od uhla dopadu, gyroskopického momentu a konštrukcie strely.
V II.oblasti začne strela rýchlo kmitať, zvyšuje sa plocha, ktorá je v styku v cieľom. V určitom bode bude strela v styku s cieľom po celej svojej dĺžke. Výsledná sila, ktorá pôsobí mimo ťažiska strely spôsobuje jej vybočenie z priameho smeru. Dochádza k vzniku dutiny. Maximálny uhol rotácie strely závisí od jej okamžitej rýchlosti a geometrických charakteristik ( tvar, štíhlosť a moment zotrvačnosti ). Vplyvom vonkajších síl môže dôjsť k deformácii strely alebo fragmentácii.
V III.oblasti strela pokračuje v kmitavom pohybe a vzniká ďalšia ale už menšia dutina. Podtlak však ťahá strelu a moment spôsobí, že strela vychádza zadnou časťou dopredu z cieľa.
Ako je možné vidieť na obrázku sú dve dutiny – primárna ( permanente wundhohle ) a sekundárna ( temporäre wundhohle ). Primárna dutina je vlastne strelný kanál, ktorý zanecháva za sebou strela. Sekundárna dutina je závislá od energie a priemeru strely. Vzniká ešte pred dopadom strely na cieľ, nakoľko je tvorená aj vybráciami, ktoré spôsobuje rázová tlaková vlna ( SDW ). Táto rázová tlaková vlna sa pohybuje pred strelou. Dôležitú úlohu tu zohráva aj kinetická energia strely, ktorá sa šíri aj v priečnom smere na smer pohybu strely. Podľa ( 4 ) pri dopade strely s približne dvojnásobnou rýchlosťou zvuku na cieľ dosahuje rázová tlaková vlna hodnotu pretlaku na hrote strely 10 MPa a šíri sa rýchlosťou 1400 – 1600 ms-1. Objem sekundárnej dutiny prevyšuje objem primárnej dutiny až 30 krát. Po počiatočnej fáze pretlaku nasleduje fáza podtlaku, čím dochádza ku kmitaniu. Kmitavý pohyb stien sekundárnej dutiny je tlmený a po útlme radiálnych síl vzniká strelný kanál.
V prípade poloplášťovej strely je hlavný rozdiel v tom, že vstupný strelný kanál takmer úplne chýba a sekundárna dutina vzniká hneď po proniknutí do cieľa ( 3 ). Pritom dochádza k extrémne rýchlej deformácii prednej časti strely v čase približne 0,1 ms. Tlak na špičke strely núti strelu k deformácii. Povrch strely, ktorý je v styku s cieľom rastie, prierezová hustota sa znižuje a prenos energie na cieľ sa zvyšuje [ 3 ] . V prípade, že dôjde k asymetrickej deformácii strely, alebo cieľ nie je homogénny, môže dôjsť k vychýleniu dráhy strely z priameho smeru. Na dokreslenie si ešte pozrime grafy balistických testov, ktoré zverejnila spoločnosť Brass Fetcher ( 5 ). Zamerali sa na analýzu rýchlosti ( m/s ) a okamžitej kinetickej energie ( J ) v bode maximálneho priemeru ( mm ) sekundárnej dutiny vybraných striel, medzi ktorými boli aj strely poľovníkom dobre známych kalibrov 22 K-Hornet ( strela s hmotnosťou 2,6 g, pri uvádzanej dopadovej rýchlosti 852 ms-1 ), 223 Remington ( strela s hmotnosťou 3,57 g, pri uvádzanej dopadovej rýchlosti 907 ms-1 ), 260 Remington ( kaliber 6,5, strela s hmotnosťou 7,8 g, pri uvádzanej dopadovej rýchlosti 785 ms-1 ), 308 Winchester ( strela s hmotnosťou 9,75 g, pri uvádzanej dopadovej rýchlosti 820 ms-1 ) a 30-06 Springfield ( strela s hmotnosťou 3,57 g, pri uvádzanej dopadovej rýchlosti 1175 ms-1 ).
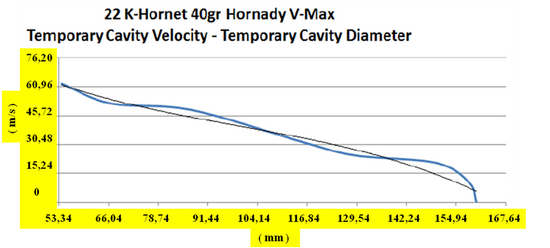
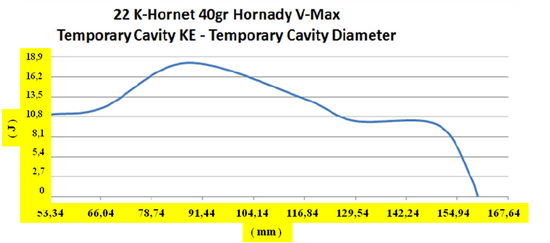
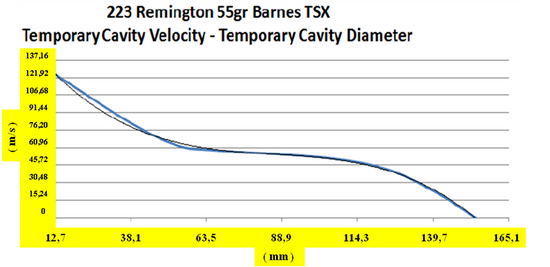
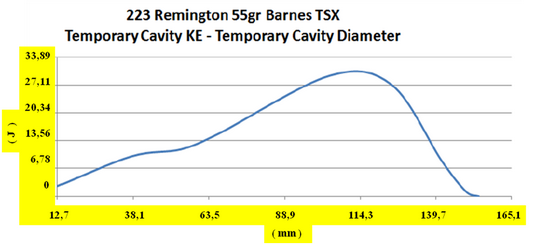
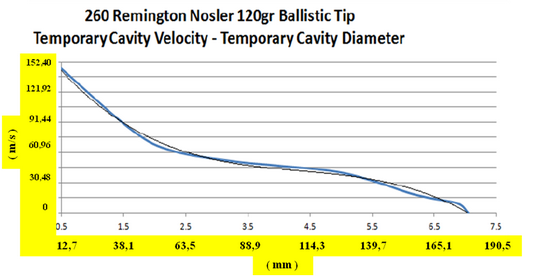
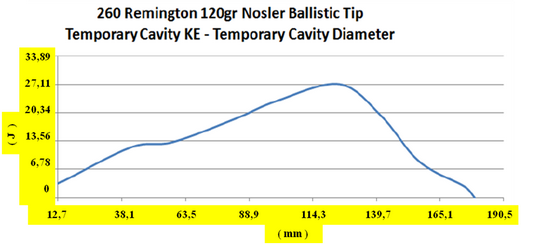
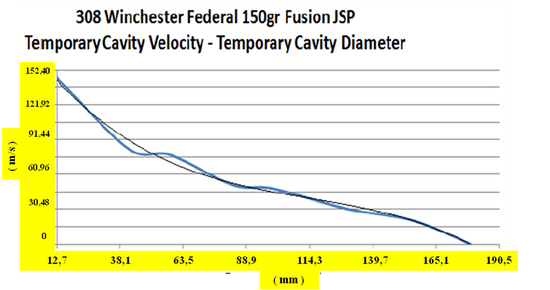
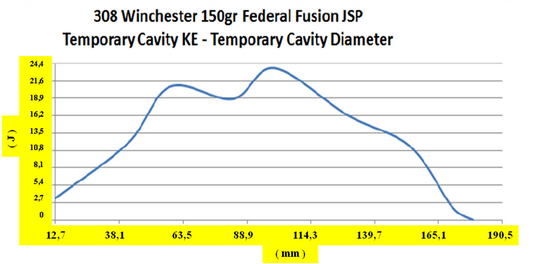
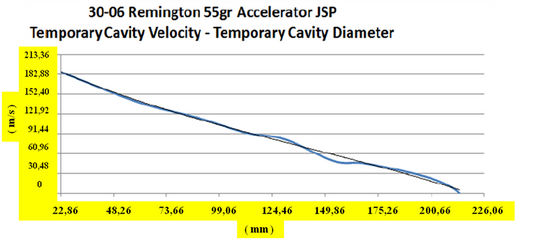
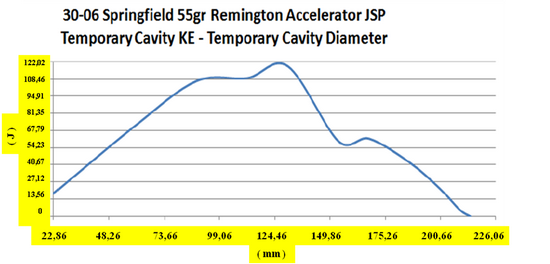
Z grafov je možné zistiť, že rýchlosť pre uvedené kalibre sa pohybuje v rozsahu 7,15 – 18,44 % hodnoty uvádzanej dopadovej rýchlosti a okamžitá kinetická energia v rozsahu 0,7 – 4,8 % dopadovej energie.
Nasledujúce dva obrázky ilustrujú typické tvary dutín pre rôzne typy brokových a guľových striel ( 2 ).
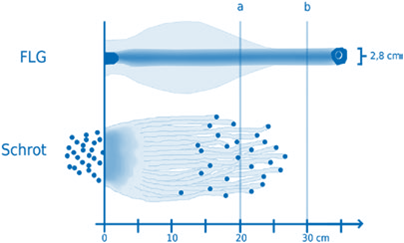
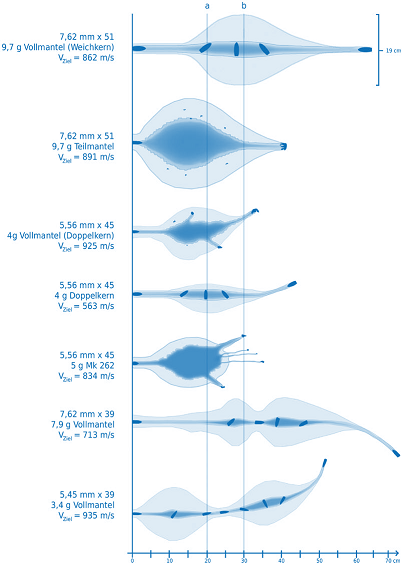
Článok si vzhľadom na zložitosť problematiky terminálnej balistiky kladie za hlavný cieľ, zjednodušenou formou priblížiť poľovníkom, čo sa deje so strelou pri dopade a jej prieniku cieľom.
(1) International Committee of the Red Cross brochure ( 2008 ) Wound Ballistics An Introduction for Healt, Legal, Forensic, Military and Law Enforcement Professionals
(2) C.Neitzel, K.Ladehof ( 2012 ) Taktische Medizin Notfallmedizin und Einsatzmedizin, Springer
(3) B.P.Kneubuehl, R.M.Coupland, M.A.Rothschild,M.J.Thali ( 2011 ) Wound Ballistic, Basic and Applications, Springer
(4) David Kotík ( 2006 ) Kriminalistická balistika a její význam v průmyslu komerční bezpečnosti, bakalárska práca, Univerzita Tomáše Bati ve Zlíně
(5) Brass Fetcher ( 2011 ) Temporary Cavity Velocity and Diameter Of representative Handgun and Rifle Cartridges In 20% Ballistic Gelatin
Autor: Ján Krnáč
